Our Experts: Jean-Chirstophe Charlier (UCLouvain), Viet-Hung Nguyen (UCLouvain) and Viet Anh Tran (UCLouvain)
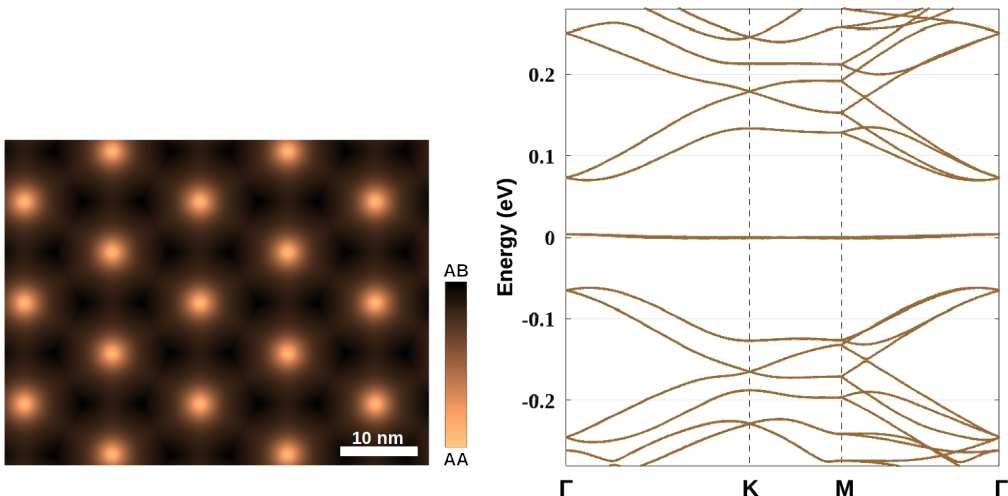
We use atomic-structure relaxation of different 2D materials in order to undertand their physical properties as a function of the twist angle. For the atomic-structure relaxation of BN/graphene layers, obtained using molecular dynamics with classical potentials, the intra-layer forces are computed using the optimized Tersoff and Brenner potentials, while inter-layer interactions are modeled using the Kolmogorov-Crespi potentials. In order to model the moiré structure created when stacking the BN handle (multi-layer h-BN) on graphene, our simulations consider a simplified atomic system consisting of a bilayer graphene coupled to a flat monolayer BN. The lattice mismatch (~1.8%) between BN and graphene is taken into account. The atomic structure is optimized until all force components are <1 meV/atom.

interlayer distance dz between the second graphene layer and BN one is presented in the two top images. The four images below illustrate the variations of the in-plane displacements Dxy in both graphene layers. At last, the two bottom images display the modification of stacking configuration between two graphene layers, by illustrating the variation of stacking vector t. t is determined as the translation vector applied locally to a C-ring of one graphene layer to recover the AA stacking configuration at the considered position, i.e., |t| = a0 and 0 for the local AB and AA stacking configurations, respectively.
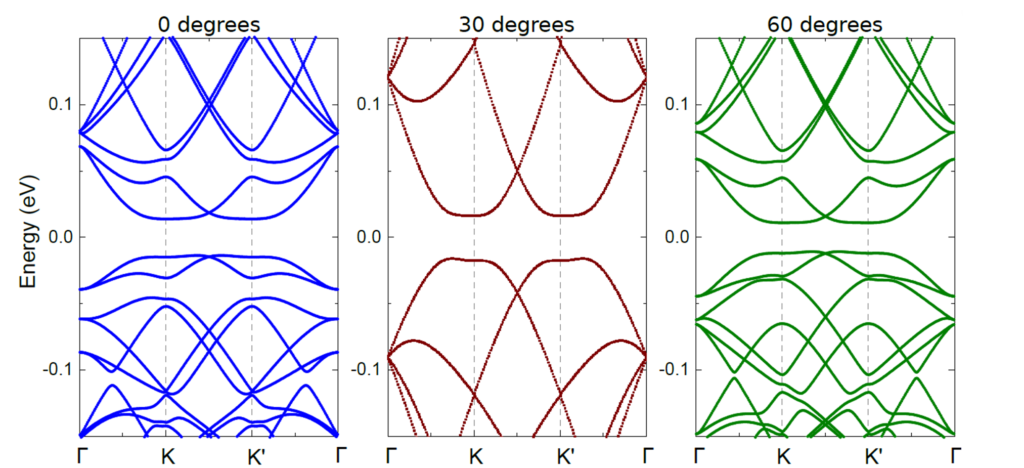
The differneces between the two alignments give rise to differences in the physical properties of the materials. To capture these differences after relaxation, the electronic structure is computed by constructing and solving the corresponding pz tight-binding Hamiltonian. The large tight-binding Hamiltonian matrix of moiré structures is diagonalized using conventional eigenvalue calculations of large-sparse matrices
More details in our recent article.
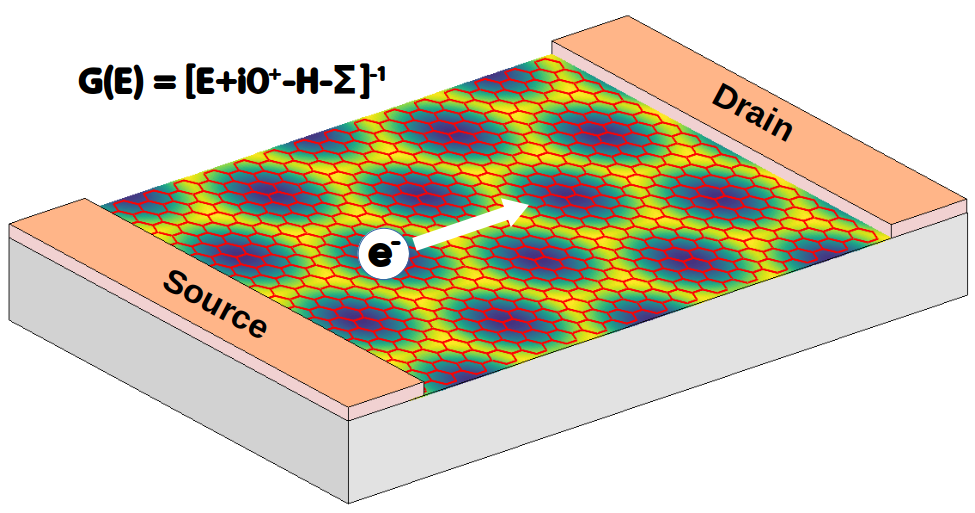
Recursive Green’s functions optimized for atomistic modelling of large superlattice-based devices
The Green’s function method is a very powerful tool for modelling electronic and transport properties in nanoscale electronic devices, including its advantage in computing the interplay between quantum confinement effects and scatterings. As atomistic calculations are generally expensive, recursive techniques have been developed to optimize the cost of Green’s function calculations. However, when computing the large superlattice devices, recursive Green’s function calculations are still facing difficult issues. Indeed, the large periodicity of superlattices make modeling of the device’s leads too heavy or even unfeasible. In such context, recursive calculations were further optimized and their applications in modeling of the electronic and transport properties of large (possibly, experimental size) superlattices, you can have more details in the article of the consortium (ArXiv).
Simulations on Twisted bilayer graphene
Moiré superlattices are theoretically investigated by multi-scale approaches. In particular, both first-principles and semi-empirical models are properly used to explore a large range of moiré cells from a few angstroms to hundreds of nanometres (for examples see: this article and this one) . Semi-empirical approaches include classical force-fields to model the atomic structure relaxation and first-principles-enriched tight-binding Hamiltonians to compute the electronic properties. These electronic models are solved using either conventional eigenvalue calculations of large-sparse matrices or recursive Green’s functions techniques.